While tools like HubSpot’s free statistical significance calculator can make the math easier, understanding what they calculate and how it impacts your strategy is invaluable.
Below, I’ll break down statistical significance with a real-world example, giving you the tools to make smarter, data-driven decisions in your marketing campaigns.
Table of Contents
What is statistical significance?
In marketing, statistical significance is when the results of your research show that the relationships between the variables you're testing (like conversion rate and landing page type) aren't random; they influence each other.
Why is statistical significance important?
Statistical significance is like a truth detector for your data. It helps you determine if the difference between any two options — like your subject lines — is likely a real or random chance.
Think of it like flipping a coin. If you flip it five times and get heads four times, does that mean your coin is biased? Probably not.
But if you flip it 1,000 times and get heads 800 times, now you might be onto something.
That's the role statistical significance plays: it separates coincidence from meaningful patterns. This was exactly what our email expert was trying to explain when I suggested we A/B test our subject lines.
Just like the coin flip example, she pointed out that what looks like a meaningful difference — say, a 2% gap in open rates — might not tell the whole story.

We needed to understand statistical significance before making decisions that could affect our entire email strategy.
She then walked me through her testing process:
- Group A would receive Subject Line A, and Group B would get Subject Line B.
- She'd track open rates for both groups, compare the results, and declare a winner.
“Seems straightforward, right?” she asked. Then she revealed where it gets tricky.
She showed me a scenario: Imagine Group A had an open rate of 25% and Group B had an open rate of 27%. At first glance, it looks like Subject Line B performed better. But can we trust this result?
What if the difference was just due to random chance and not because Subject Line B was truly better?
This question led me down a fascinating path to understand why statistical significance matters so much in marketing decisions. Here's what I discovered:
Here's Why Statistical Significance Matters
- Sample size influences reliability: My initial assumption about our 5,000 subscribers being enough was wrong. When split evenly between the two groups, each subject line would only be tested on 2,500 people. With an average open rate of 20%, we‘d only see around 500 opens per group. I learned that’s not a huge number when trying to detect small differences like a 2% gap. The smaller the sample, the higher the chance that random variability skews your results.
- The difference might not be real: This was eye-opening for me. Even if Subject Line B had 10 more opens than Subject Line A, that doesn‘t mean it’s definitively better. A statistical significance test would help determine if this difference is meaningful or if it could have happened by chance.
- Making the wrong decision is costly: This really hits home. If we falsely concluded that Subject Line B was better and used it in future campaigns, we might miss opportunities to engage our audience more effectively. Worse, we could waste time and resources scaling a strategy that doesn't actually work.
Through my research, I discovered that statistical significance helps you avoid acting on what could be a coincidence. It asks a crucial question: ‘If we repeated this test 100 times, how likely is it that we’d see this same difference in results?'
If the answer is ‘very likely,’ then you can trust the outcome. If not, it's time to rethink your approach.
Though I was eager to learn the statistical calculations, I first needed to understand a more fundamental question: when should we even run these tests in the first place?

How to Test for Statistical Significance: My Quick Decision Framework
When deciding whether to run a test, use this decision framework to assess whether it’s worth the time and effort. Here’s how I break it down.
Run tests when:
- You have a sufficient sample size. The test can reach statistical significance based on the number of users or recipients.
- The change could impact business metrics. For example, testing a new call-to-action could directly improve conversions.
- When you can wait for the full test duration. Impatience can lead to inconclusive results. I always ensure the test has enough time to run its course.
- The difference would justify implementation cost. If the results lead to a meaningful ROI or reduced resource costs, it’s worth testing.
Don’t run the test when:
- The sample size is too small. Without enough data, the results won’t be reliable or actionable.
- You need immediate results. If a decision is urgent, testing may not be the best approach.
- The change is minimal. Testing small tweaks, like moving a button a few pixels, often requires enormous sample sizes to show meaningful results.
- Implementation cost exceeds potential benefit. If the resources needed to implement the winning version outweigh the expected gains, testing isn’t worth it.
Test Prioritization Matrix
When you’re juggling multiple test ideas, I recommend using a prioritization matrix to focus on high-impact opportunities.
High-priority tests:
- High-traffic pages. These pages offer the largest sample sizes and quickest path to significance.
- Major conversion points. Test areas like sign-up forms or checkout processes that directly affect revenue.
- Revenue-generating elements. Headlines, CTAs, or offers that drive purchases or subscriptions.
- Customer acquisition touchpoints. Email subject lines, ads, or landing pages that influence lead generation.
Low-priority tests:
- Low-traffic pages. These pages take much longer to produce actionable results.
- Minor design elements. Small stylistic changes often don’t move the needle enough to justify testing.
- Non-revenue pages. About pages or blogs without direct links to conversions may not warrant extensive testing.
- Secondary metrics. Testing for vanity metrics like time on page may not align with business goals.
This framework ensures you focus your efforts where they matter most.

But this led to my next big question: once you've decided to run a test, how do you actually determine statistical significance?
Thankfully, while the math might sound intimidating, there are simple tools and methods for getting accurate answers. Let's break it down step by step.
How to Calculate and Determine Statistical Significance
- Decide what you want to test.
- Determine your hypothesis.
- Start collecting your data.
- Calculate chi-squared results.
- Calculate your expected values.
- See how your results differ from what you expected.
- Find your sum.
- Interpret your results.
- Determine statistical significance.
- Report on statistical significance to your team.
1. Decide what you want to test.
The first step is to identify what you’d like to test. This could be:
- Comparing conversion rates on two landing pages with different images.
- Testing click-through rates on emails with different subject lines.
- Evaluating conversion rates on different call-to-action buttons at the end of a blog post.
The possibilities are endless, but simplicity is key. Start with a specific piece of content you want to improve, and set a clear goal — for example, boosting conversion rates or increasing views.
While you can explore more complex approaches, like testing multiple variations (multivariate tests), I recommend starting with a straightforward A/B test. For this example, I’ll compare two variations of a landing page with the goal of increasing conversion rates.
Pro tip: If you’re curious about the difference between A/B and multivariate tests, check out this guide on A/B vs. Multivariate Testing.
2. Determine your hypothesis.
When it comes to A/B testing, our resident email expert always emphasizes starting with a clear hypothesis. She explained that having a hypothesis helps focus the test and ensures meaningful results.
A strong hypothesis should clearly state what you're testing and what outcome you expect. For example, when testing email subject lines, your hypothesis might be: "Using action verbs in subject lines will increase email open rates by at least 10% compared to subject lines without action verbs."
Another key step is deciding on a confidence level before the test begins. Most tests use a 95% confidence level, which ensures the results are statistically reliable and not due to random chance.
This structured approach makes it easier to interpret your results and take meaningful action.
3. Start collecting your data.
Once you’ve determined what you’d like to test, it’s time to start collecting your data. Since the goal of this test is to figure out which subject line performs better for future campaigns, you’ll need to select an appropriate sample size.
For emails, this might mean splitting your list into random sample groups and sending each group a different subject line variation.
For instance, if you’re testing two subject lines, divide your list evenly and randomly to ensure both groups are comparable.
Determining the right sample size can be tricky, as it varies with each test. A good rule of thumb is to aim for an expected value greater than 5 for each variation.
This helps ensure your results are statistically valid. (I’ll cover how to calculate expected values further down.)
4. Calculate Chi-Squared results.
In researching how to analyze our email testing results, I discovered that while there are several statistical tests available, the Chi-Squared test is particularly well-suited for A/B testing scenarios like ours.
This made perfect sense for our email testing scenario. A Chi-Squared test is used for discrete data, which simply means the results fall into distinct categories.
In our case, an email recipient will either open the email or not open it — there's no middle ground.
One key concept I needed to understand was the confidence level (also referred to as the alpha of the test). A 95% confidence level is standard, meaning there's only a 5% chance (alpha = 0.05) that the observed relationship is due to random chance.
For example: “The results are statistically significant with 95% confidence” indicates that the alpha was 0.05, meaning there's a 1 in 20 chance of error in the results.
My research showed that organizing the data into a simple chart for clarity is the best way to start.
Since I’m testing two variations (Subject Line A and Subject Line B) and two outcomes (opened, did not open), I can use a 2x2 chart:
|
Outcome |
Subject Line A |
Subject Line B |
Total |
|
Opened |
X (e.g., 125) |
Y (e.g., 135) |
X + Y |
|
Did Not Open |
Z (e.g., 375) |
W (e.g., 365) |
Z + W |
|
Total |
X + Z |
Y + W |
N |
This makes it easy to visualize the data and calculate your Chi-Squared results. Totals for each column and row provide a clear overview of the outcomes in aggregate, setting you up for the next step: running the actual test.
While tools like HubSpot's A/B Testing Kit can calculate statistical significance automatically, understanding the underlying process helps you make better testing decisions. Let's look at how these calculations actually work:
Running the Chi-Squared test
Once I’ve organized my data into a chart, the next step is to calculate statistical significance using the Chi-Squared formula.
Here’s what the formula looks like:
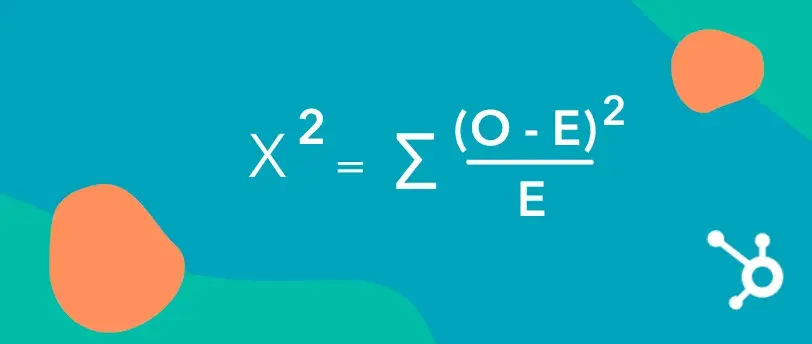
In this formula:
- Σ means to sum (add up) all calculated values.
- O represents the observed (actual) values from your test.
- E represents the expected values, which you calculate based on the totals in your chart.
To use the formula:
- Subtract the expected value (E) from the observed value (O) for each cell in the chart.
- Square the result.
- Divide the squared difference by the expected value (E).
- Repeat these steps for all cells, then sum up all the results after the Σ to get your Chi-Squared value.
This calculation tells you whether the differences between your groups are statistically significant or likely due to chance.
5. Calculate your expected values.
Now, it’s time to calculate the expected values (E) for each outcome in your test. If there’s no relationship between the subject line and whether an email is opened, we’d expect the open rates to be proportionate across both variations (A and B).
Let’s assume:
- Total emails sent = 5,000
- Total opens = 1,000 (20% open rate)
- Subject Line A was sent to 2,500 recipients.
- Subject Line B was also sent to 2,500 recipients.
Here’s how you organize the data in a table:
|
Outcome |
Subject Line A |
Subject Line B |
Total |
|
Opened |
500 (O) |
500 (O) |
1,000 |
|
Did Not Open |
2,000 (O) |
2,000 (O) |
4,000 |
|
Total |
2,500 |
2,500 |
5,000 |
Expected Values (E):
To calculate the expected value for each cell, use this formula:
E=(Row Total×Column Total)Grand TotalE = \frac{(\text{Row Total} \times \text{Column Total})}{\text{Grand Total}}E=Grand Total(Row Total×Column Total)
For example, to calculate the expected number of opens for Subject Line A:
E=(1,000×2,500)5,000=500E = \frac{(1,000 \times 2,500)}{5,000} = 500E=5,000(1,000×2,500)=500
Repeat this calculation for each cell:
|
Outcome |
Subject Line A (E) |
Subject Line B (E) |
Total |
|
Opened |
500 |
500 |
1,000 |
|
Did Not Open |
2,000 |
2,000 |
4,000 |
|
Total |
2,500 |
2,500 |
5,000 |
These expected values now provide the baseline you’ll use in the Chi-Squared formula to compare against the observed values.
6. See how your results differ from what you expected.
To calculate the Chi-Square value, compare the observed frequencies (O) to the expected frequencies (E) in each cell of your table. The formula for each cell is:
χ2=(O−E)2E\chi^2 = \frac{(O - E)^2}{E}χ2=E(O−E)2
Steps:
- Subtract the observed value from the expected value.
- Square the result to amplify the difference.
- Divide this squared difference by the expected value.
- Sum up all the results for each cell to get your total Chi-Square value.
Let’s work through the data from the earlier example:
|
Outcome |
Subject Line A (O) |
Subject Line B (O) |
Subject Line A (E) |
Subject Line B (E) |
(O−E)2/E(O - E)^2 / E(O−E)2/E |
|
Opened |
550 |
450 |
500 |
500 |
(550−500)2/500=5(550-500)^2 / 500 = 5(550−500)2/500=5 |
|
Did Not Open |
1,950 |
2,050 |
2,000 |
2,000 |
(1950−2000)2/2000=1.25(1950-2000)^2 / 2000 = 1.25(1950−2000)2/2000=1.25 |
Now sum up the (O−E)2/E(O - E)^2 / E(O−E)2/E values:
χ2=5+1.25=6.25\chi^2 = 5 + 1.25 = 6.25χ2=5+1.25=6.25
This is your total Chi-Square value, which indicates how much the observed results differ from what was expected.
What does this value mean?
You’ll now compare this Chi-Square value to a critical value from a Chi-Square distribution table based on your degrees of freedom (number of categories - 1) and confidence level. If your value exceeds the critical value, the difference is statistically significant.
7. Find your sum.
Finally, I sum the results from all cells in the table to get my Chi-Square value. This value represents the total difference between the observed and expected results.
Using the earlier example:
|
Outcome |
(O−E)2/E(O - E)^2 / E(O−E)2/E for Subject Line A |
(O−E)2/E(O - E)^2 / E(O−E)2/E for Subject Line B |
|
Opened |
5 |
5 |
|
Did Not Open |
1.25 |
1.25 |
χ2=5+5+1.25+1.25=12.5\chi^2 = 5 + 5 + 1.25 + 1.25 = 12.5χ2=5+5+1.25+1.25=12.5
Compare your Chi-Square value to the distribution table.
To determine if the results are statistically significant, I compare the Chi-Square value (12.5) to a critical value from a Chi-Square distribution table, based on:
- Degrees of freedom (df): This is determined by (number of rows −1)×(number of columns −1)(number\ of\ rows\ - 1) \times (number\ of\ columns\ - 1)(number of rows −1)×(number of columns −1). For a 2x2 table, df=1df = 1df=1.
- Alpha (α\alphaα): The confidence level of the test. With an alpha of 0.05 (95% confidence), the critical value for df=1df = 1df=1 is 3.84.
In this case:
- Chi-Square Value = 12.5
- Critical Value = 3.84
Since 12.5>3.8412.5 > 3.8412.5>3.84, the results are statistically significant. This indicates that there is a relationship between the subject line and the open rate.
If the Chi-Square value were lower…
For example, if the Chi-Square value had been 0.95 (as in the original scenario), it would be less than 3.84, meaning the results would not be statistically significant. This would indicate no meaningful relationship between the subject line and the open rate.
8. Interpret your results.
As I dug deeper into statistical testing, I learned that interpreting results properly is just as crucial as running the tests themselves. Through my research, I discovered a systematic approach to evaluating test outcomes.
Strong Results (act immediately)
Results are considered strong and actionable when they meet these key criteria:
- 95%+ confidence level. The results are statistically significant with minimal risk of being due to chance.
- Consistent results across segments. Performance holds steady across different user groups or demographics.
- A clear winner emerges. One version consistently outperforms the other.
- Matches business logic. The results align with expectations or reasonable business assumptions.
When results meet these criteria, the best practice is to act quickly: implement the winning variation, document what worked, and plan follow-up tests for further optimization.
Weak Results (need more data)
On the flip side, results are typically considered weak or inconclusive when they show these characteristics:
- Below 95% confidence level. The results don't meet the threshold for statistical significance.
- Inconsistent across segments. One version performs well with certain groups but poorly with others.
- No clear winner. Both variations show similar performance without a significant difference.
- Contradicts previous tests. Results differ from past experiments without a clear explanation.
In these cases, the recommended approach is to gather more data through retesting with a larger sample size or extending the test duration.
Next Steps Decision Tree
My research revealed a practical decision framework for determining next steps after interpreting results.
If the results are significant:
- Implement the winning version. Roll out the better-performing variation.
- Document learnings. Record what worked and why for future reference.
- Plan follow-up tests. Build on the success by testing related elements (e.g., testing headlines if subject lines performed well).
- Scale to similar areas. Apply insights to other campaigns or channels.
If the results are not significant:
- Continue with the current version. Stick with the existing design or content.
- Plan a larger sample test. Revisit the test with a larger audience to validate the findings.
- Test bigger changes. Experiment with more dramatic variations to increase the likelihood of a measurable impact.
- Focus on other opportunities. Redirect resources to higher-priority tests or initiatives.
This systematic approach ensures that every test, whether significant or not, contributes valuable insights to the optimization process.
9. Determine statistical significance.
Through my research, I discovered that determining statistical significance comes down to understanding how to interpret the Chi-Square value. Here's what I learned.
Two key factors determine statistical significance:
- Degrees of freedom (df). This is calculated based on the number of categories in the test. For a 2x2 table, df=1.
- Critical value. This is determined by the confidence level (e.g., 95% confidence has an alpha of 0.05).
Comparing values:
The process turned out to be quite straightforward: you compare your calculated Chi-Square value to the critical value from a Chi-Square distribution table. For example, with df=1 and a 95% confidence level, the critical value is 3.84.
What the numbers tell you:
- If your Chi-Square value is greater than or equal to the critical value, your results are statistically significant. This suggests the observed differences are real and not due to random chance.
- If your Chi-Square value is less than the critical value, your results aren't statistically significant, indicating the observed differences could be due to random chance.
What happens if the results aren't significant? Through my investigation, I learned that non-significant results aren‘t necessarily failures — they’re common and provide valuable insights. Here's what I discovered about handling such situations.
Review the test setup:
- Was the sample size sufficient?
- Were the variations distinct enough?
- Did the test run long enough?
Making decisions with non-significant results:
When results aren't significant, there are several productive paths forward.
- Run another test with a larger sample size.
- Test for more dramatic variations that might show clearer differences.
- Use the data as a baseline for future experiments.
10. Report on statistical significance to your team.
After running your experiment, it’s essential to communicate the results to your team so everyone understands the findings and agrees on the next steps.
Using the email subject line example, here’s how I’d approach reporting.
- If results are not significant: I would inform my team that the test results indicate no statistically significant difference between the two subject lines. This means the subject line choice is unlikely to impact open rates for future campaigns. We could either retest with a larger sample size or move forward with either subject line.
- If the results are significant: I would explain that Subject Line A performed significantly better than Subject Line B, with a statistical significance of 95%. Based on this outcome, we should use Subject Line A for our upcoming campaign to maximize open rates.
When you’re reporting your findings, here are some best practices.
- Use clear visuals: Include a summary table or chart that compares observed and expected values alongside the calculated Chi-Square value.
- Explain the implications: Go beyond the numbers to clarify how the results will inform future decisions.
- Propose next steps: Whether implementing the winning variation or planning follow-up tests, ensure your team knows what to do.
By presenting results in a clear and actionable way, you help your team make data-driven decisions with confidence.
From Simple Test to Statistical Journey: What I Learned About Data-Driven Marketing
What started as a simple desire to test two email subject lines led me down a fascinating path into the world of statistical significance.
While my initial instinct was to just split our audience and compare results, I discovered that making truly data-driven decisions requires a more nuanced approach.
Three key insights transformed how I think about A/B testing:
First, sample size matters more than I initially thought. What seems like a large enough audience (even 5,000 subscribers!) might not actually give you reliable results, especially when you're looking for small but meaningful differences in performance.
Second, statistical significance isn‘t just a mathematical hurdle — it’s a practical tool that helps prevent costly mistakes. Without it, we risk scaling strategies based on coincidence rather than genuine improvement.
Finally, I learned that “failed” tests aren‘t really failures at all. Even when results aren’t statistically significant, they provide valuable insights that help shape future experiments and keep us from wasting resources on minimal changes that won't move the needle.
This journey has given me a new appreciation for the role of statistical rigor in marketing decisions.
While the math might seem intimidating at first, understanding these concepts makes the difference between guessing and knowing — between hoping our marketing works and being confident it does.
Editor's note: This post was originally published in April 2013 and has been updated for comprehensiveness.
a-b-testing


.png)


![How I Use Landing Page Split Testing to Find Untapped Marketing Potential [+ 12 Places to Start]](https://53.fs1.hubspotusercontent-na1.net/hubfs/53/landing-page-split-testing-1-20250121-3573417.webp)






.png)